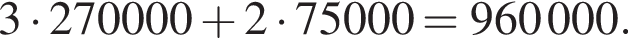Точки A, B, C лежат на большой окружности сферы так, что треугольник ABC — равносторонний. Если AB = ![]() то площадь сферы равна:
то площадь сферы равна:
Найдите значение выражения 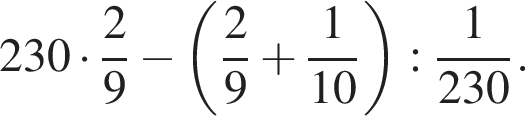
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Прямоугольный треугольник с катетами, равными 1 и ![]() вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения
вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения ![]() где V — объём фигуры вращения.
где V — объём фигуры вращения.
Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC, CA в указанном порядке находятся в отношении 9 : 5 : 4. Найдите градусную меру угла ABC.
Найдите значение выражения НОК(14, 21, 42)+НОД(36,45).
В ромб площадью ![]() вписан круг площадью 3π. Сторона ромба равна:
вписан круг площадью 3π. Сторона ромба равна:
Одно число меньше другого на 72, что составляет 18% большего числа. Найдите меньшее число.
Точка A движется по периметру треугольника KMP. Точки K1, M1, P1 лежат на медианах треугольника KMP и делят их в отношении 11 : 3, считая от вершин. По периметру треугольника K1M1P1 движется точка B со скоростью, в пять раз большей, чем скорость точки A. Сколько раз точка B обойдет по периметру треугольник K1M1P1 за то время, за которое точка A два раза обойдет по периметру треугольник KMP?
Если 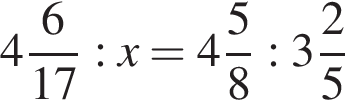 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 127°, ∠BOM = 153°. Найдите величину угла BOC.
Если 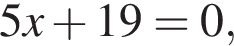 то
то  равно:
равно:
Четырехугольник MNPK, в котором ∠N=132°, вписан в окружность. Найдите градусную меру угла K.
Найдите количество всех целых решений неравенства 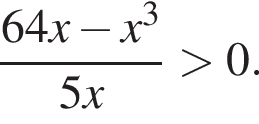
Найдите сумму корней уравнения
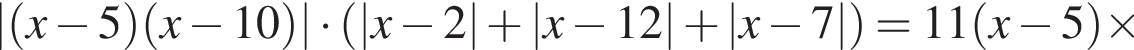
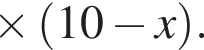
Решите неравенство 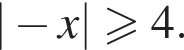
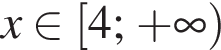
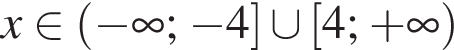
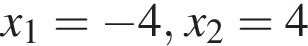

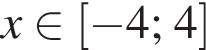
Результат разложения многочлена x (6a − b) + b − 6a на множители имеет вид:
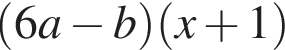
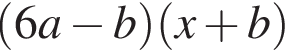
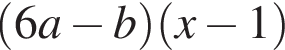
Решите уравнение 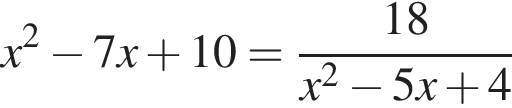 и найдите сумму его корней.
и найдите сумму его корней.
Пусть (x1; y1), (x2; y2) — решения системы уравнений 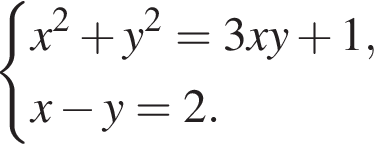
Найдите значение выражения x1x2 + y1y2.
Найдите сумму целых решений (решение, если оно единственное) системы неравенств 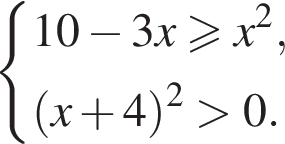
Используя рисунок, определите верное утверждение и укажите его номер.


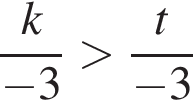
Найдите значение выражения 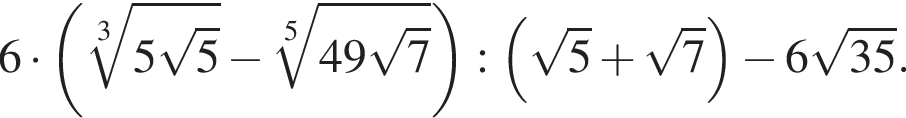
Упростите выражение 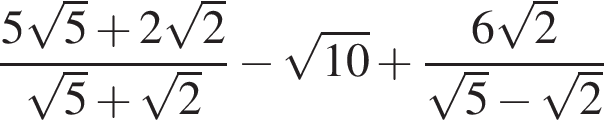
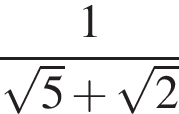
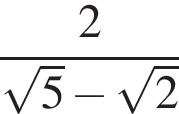
Сумма корней (корень, если он единственный) уравнения 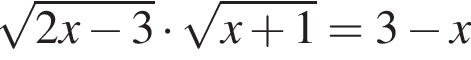 равна (равен):
равна (равен):
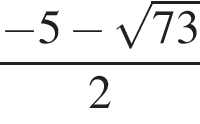
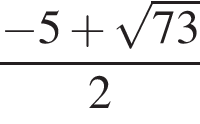
Запишите (11x)y в виде степени с основанием 11.
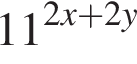
Найдите сумму корней уравнения 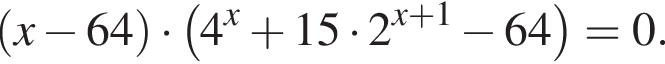
Найдите наибольшее целое решение неравенства 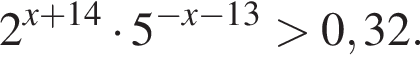
Пусть 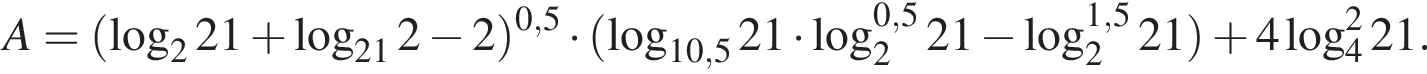
Найдите значение выражения 2A.
Корень уравнения
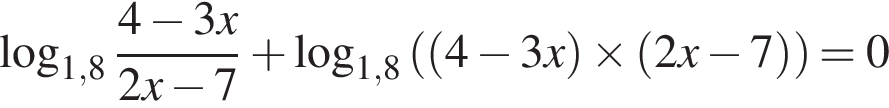
(или сумма корней, если их несколько) принадлежит промежутку:
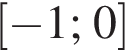
Найдите сумму наименьшего и наибольшего целых решений неравенства 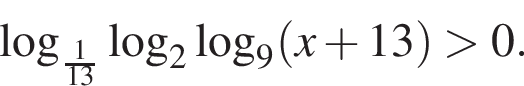
Упростите выражение 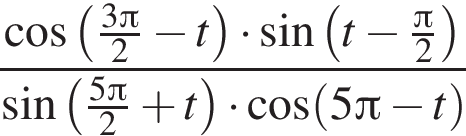
Найдите значение выражения 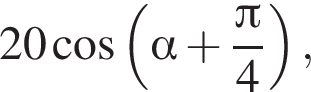 если
если 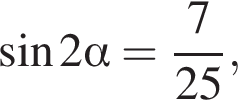
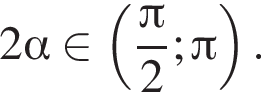
Найдите (в градусах) наибольший отрицательный корень уравнения 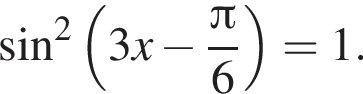
Количество целых решений неравенства 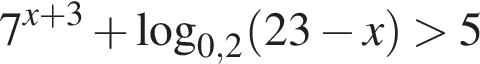 равно ...
равно ...
Количество целых решений неравенства 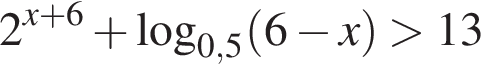 равно ...
равно ...
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
Найдите сумму целых значений x, принадлежащих области определения функции
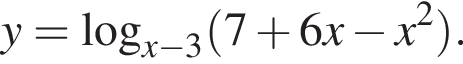
Среди точек
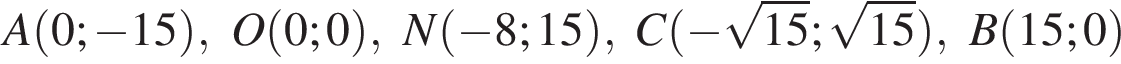 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
На диаграмме показано количество покупателей в период проведения акции в магазине. В какой день количество покупателей товара по акции составило менее 30% от количества всех покупателей в этот день?
По двум перпендикулярным прямым, которые пересекаются в точке O, движутся две точки M1 и M2 по направлению к точке O со скоростями 1 ![]() и 2
и 2 ![]() соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 4 м, M2O = 13 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 4 м, M2O = 13 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
Сумма наибольшего и наименьшего значений функции
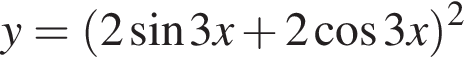
равна:
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 5 дм, после чего площадь оставшейся части листа оказалась равной 24 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Для покраски стен общей площадью 175 м2 планируется закупка краски. Объем и стоимость банок с краской приведены в таблице.
| Объем банки (в литрах) | Стоимость банки с краской (в рублях) |
|---|---|
| 2,5 | 75 000 |
| 10 | 270 000 |
Какую минимальную сумму (в рублях) потратят на покупку необходимого количества краски, если ее расход составляет 0,2 л/м2?
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.

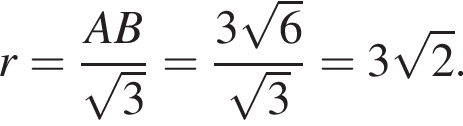 Площадь сферы равна
Площадь сферы равна 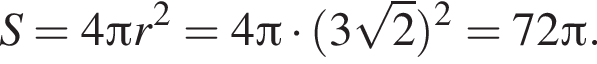
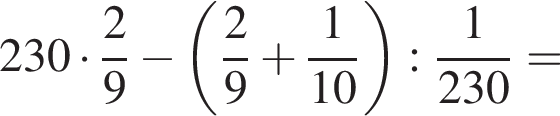
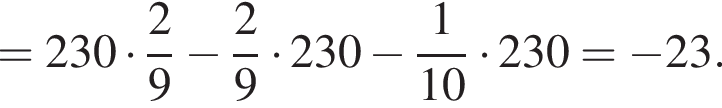
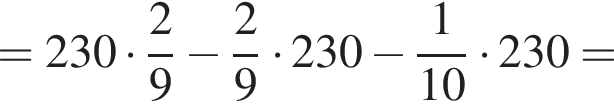
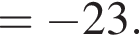
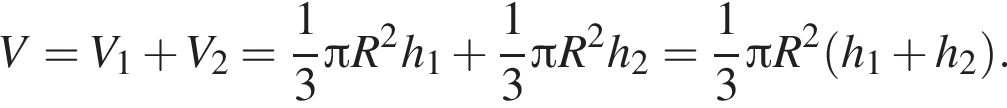
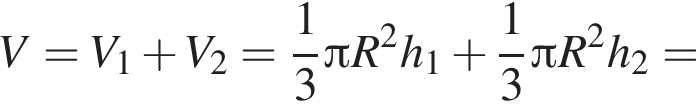
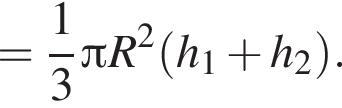
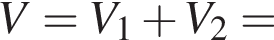
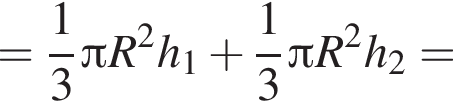
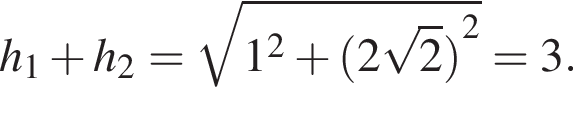
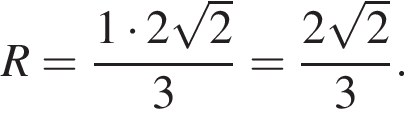
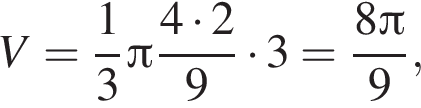 откуда
откуда 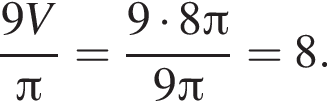
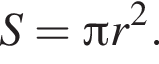 Следовательно, радиус круга равен:
Следовательно, радиус круга равен: 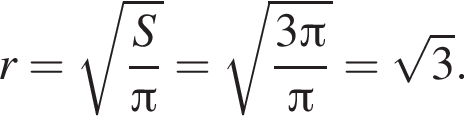 Площадь ромба равна произведению высоты на его сторону:
Площадь ромба равна произведению высоты на его сторону:  Тогда:
Тогда: 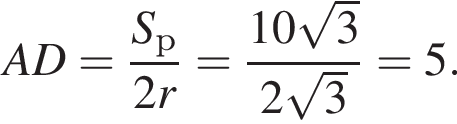
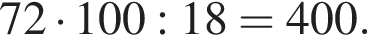 Таким образом, меньшее число
Таким образом, меньшее число 
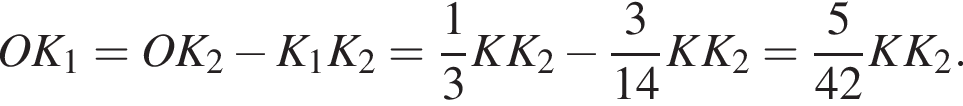
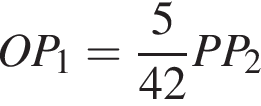 и
и 
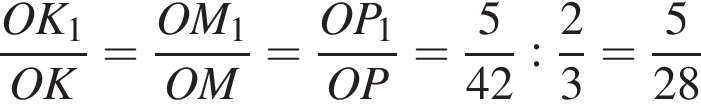 и треугольники M1K1P1 и MKP подобны, получаем
и треугольники M1K1P1 и MKP подобны, получаем 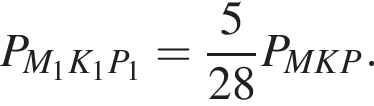 Тогда
Тогда 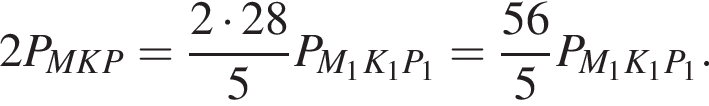 Тогда точка B обойдет периметр 56 раз.
Тогда точка B обойдет периметр 56 раз.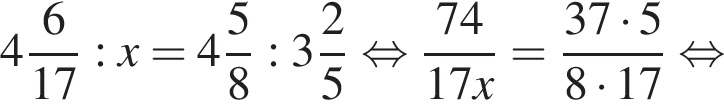
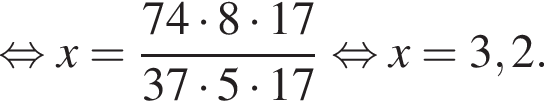
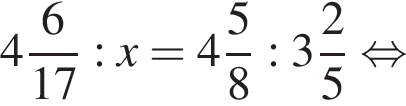
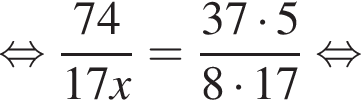
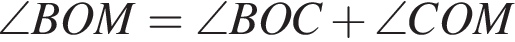 и
и  Таким образом:
Таким образом:
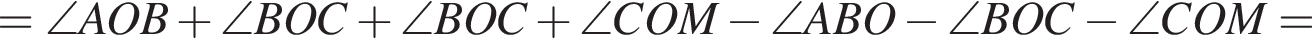
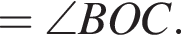

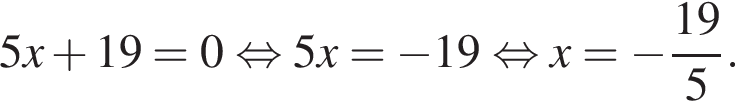
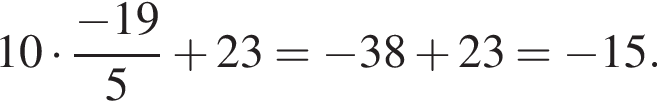

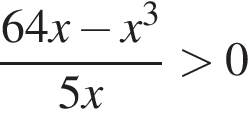
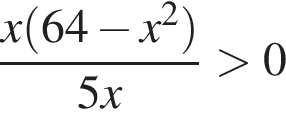
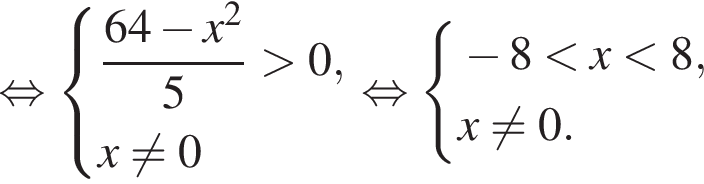
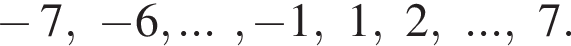
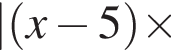
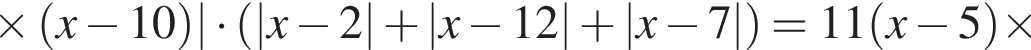
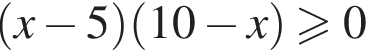 :
: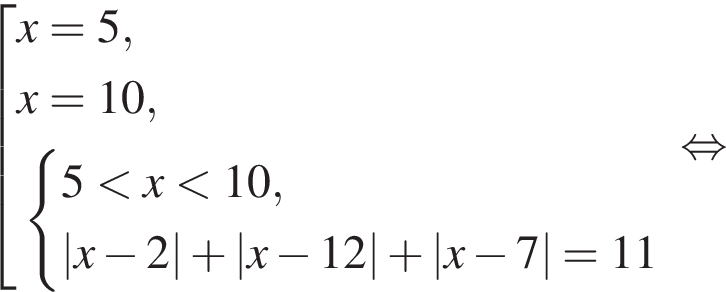
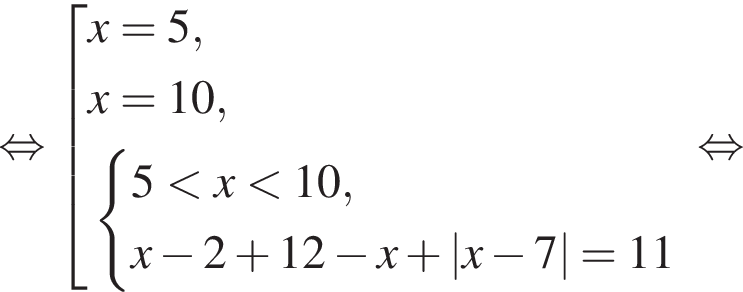
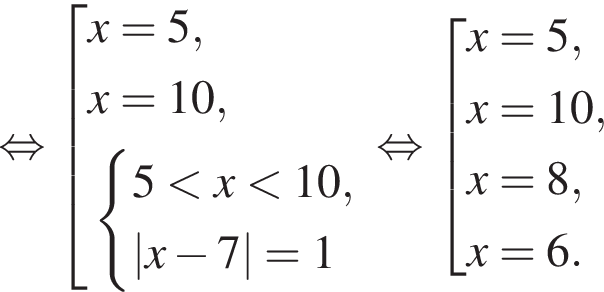

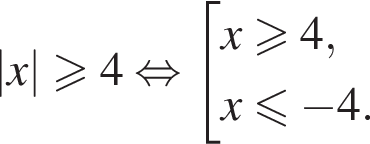

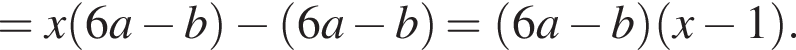

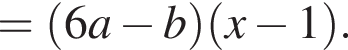
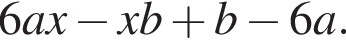
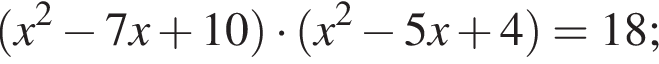


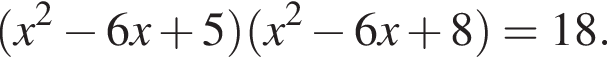
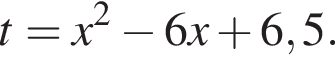 Получим:
Получим: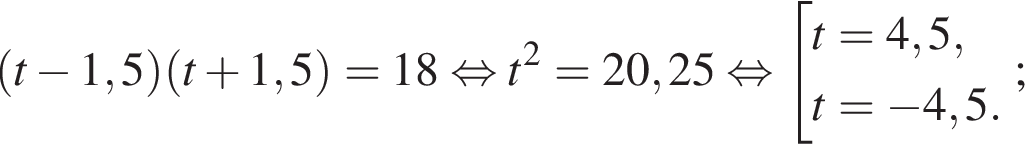
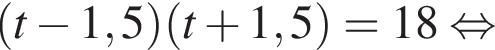
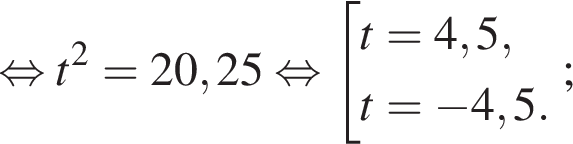
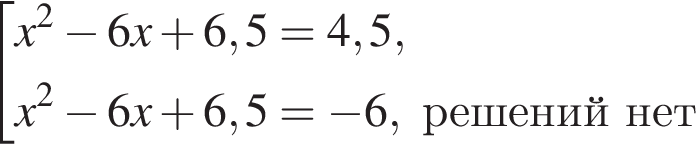
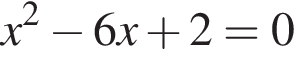 найдем по теореме Виета, она равна 6.
найдем по теореме Виета, она равна 6.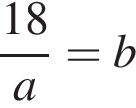 равносильно уравнению
равносильно уравнению  искать ОДЗ не требуется.
искать ОДЗ не требуется.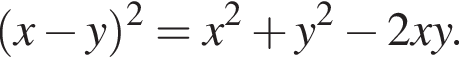 Решим систему:
Решим систему: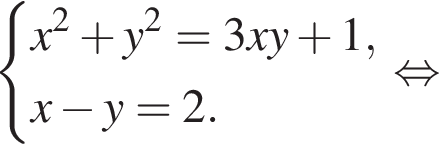
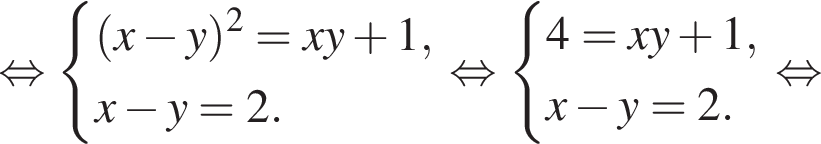
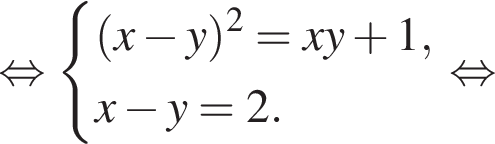
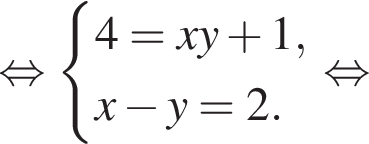
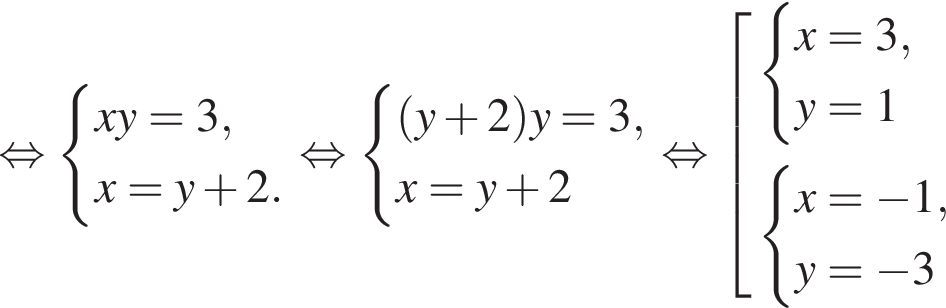
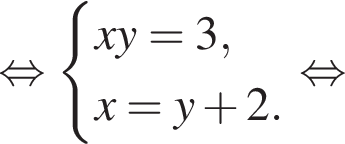
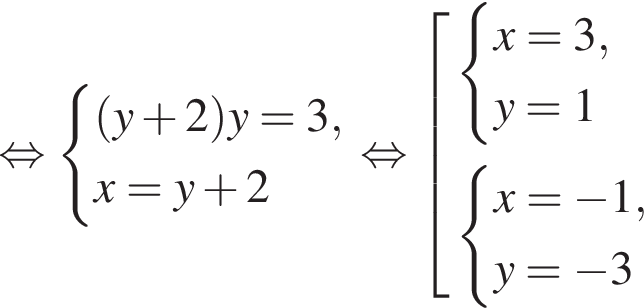
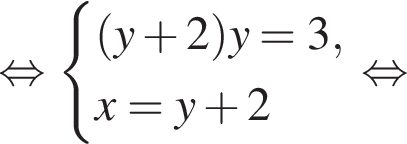
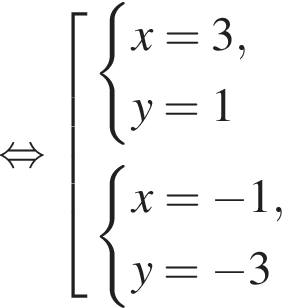
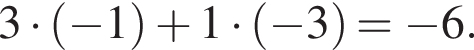

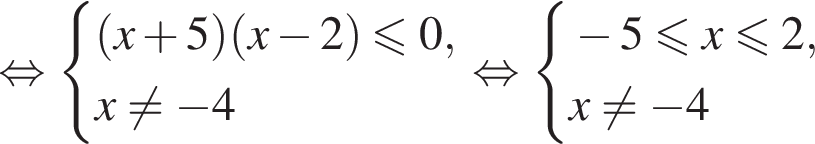
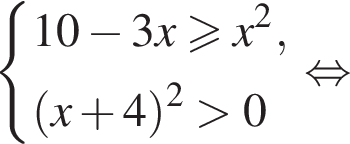
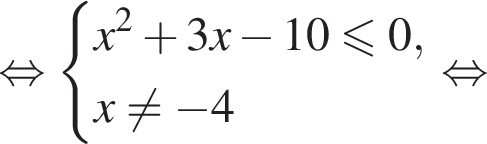
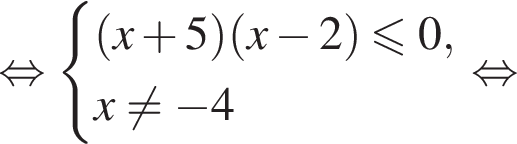
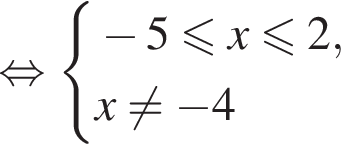
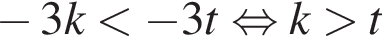 — неверно.
— неверно.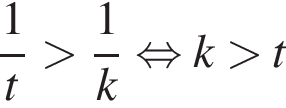 — неверно.
— неверно.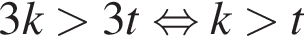 — неверно.
— неверно.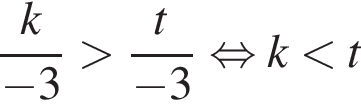 — верно.
— верно.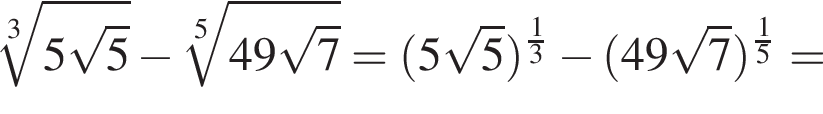
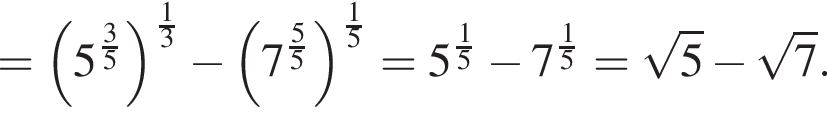
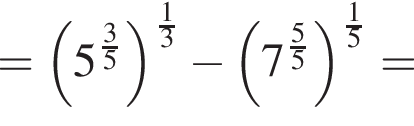
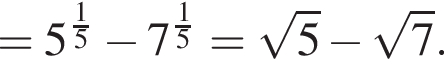
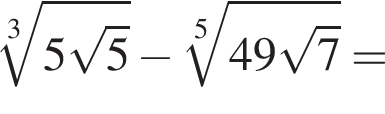
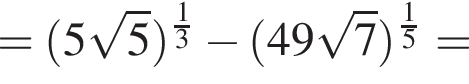
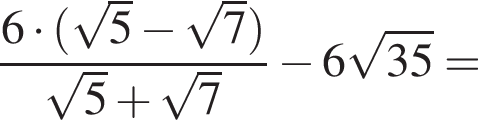
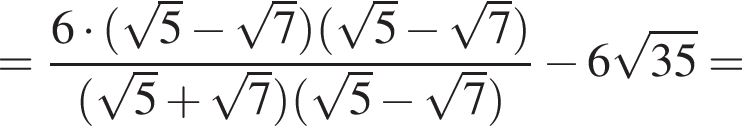
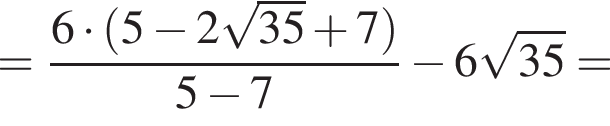
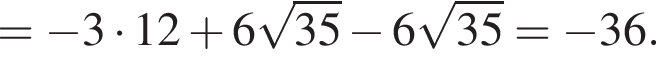
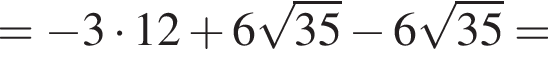
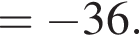
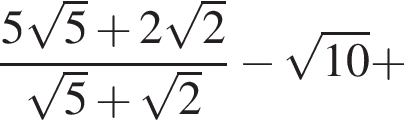
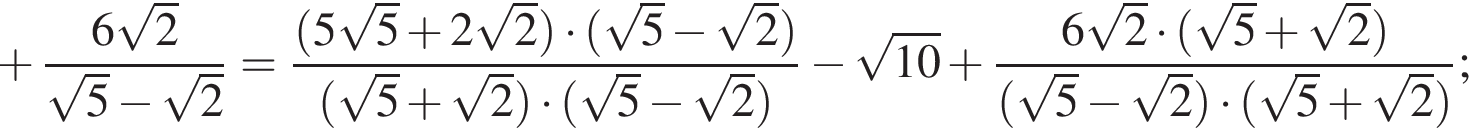
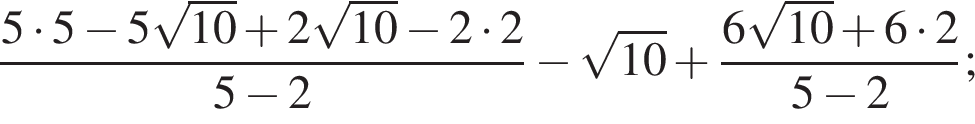
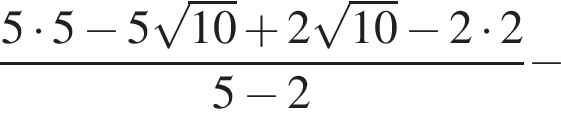
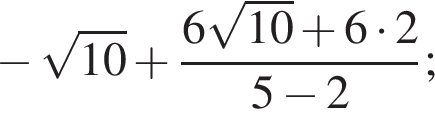
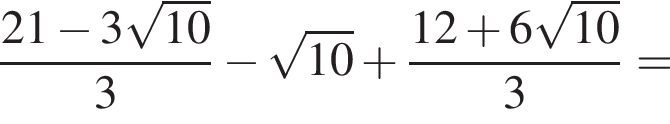
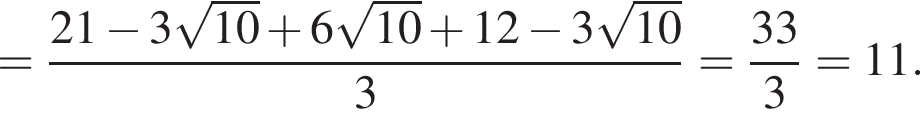
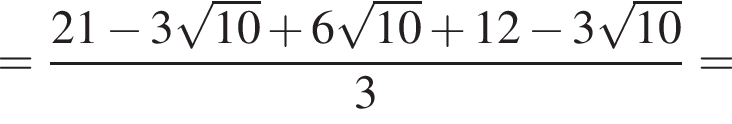
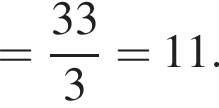
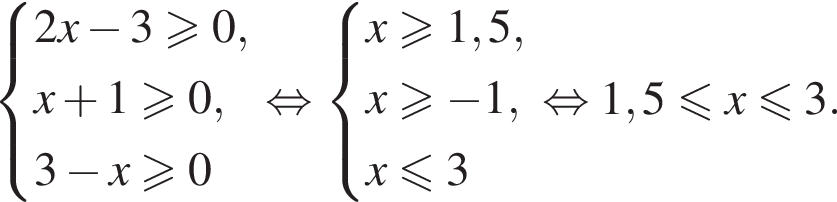
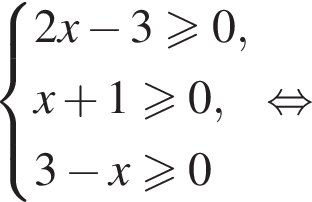
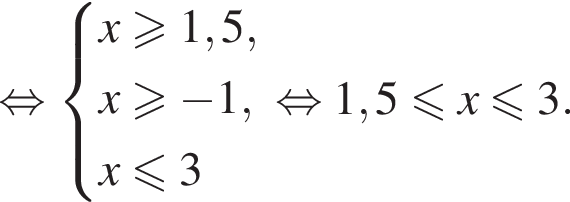
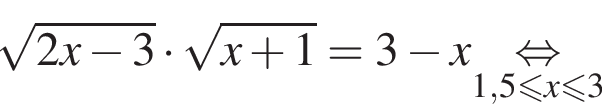
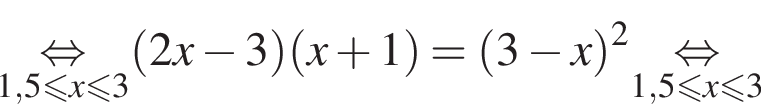
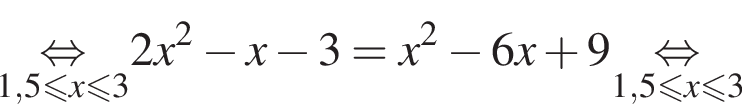
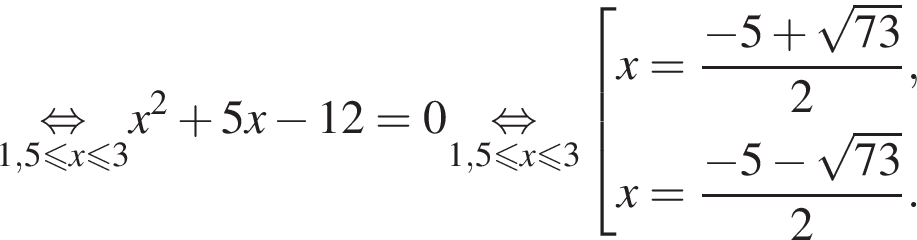
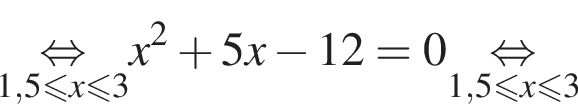
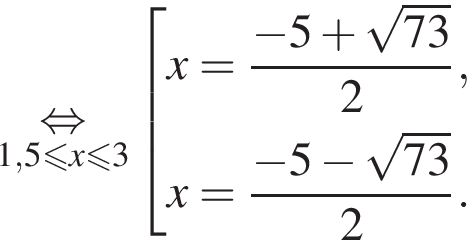
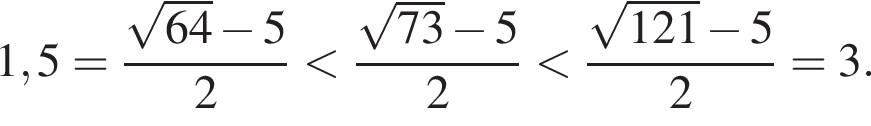
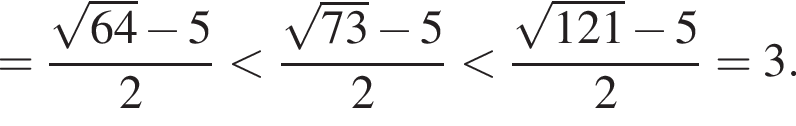
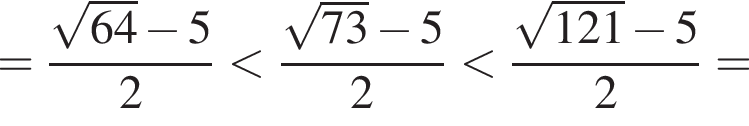
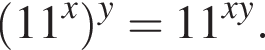
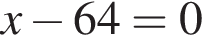 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 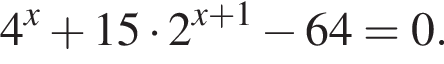 Сделаем замену
Сделаем замену 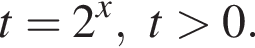 Тогда:
Тогда: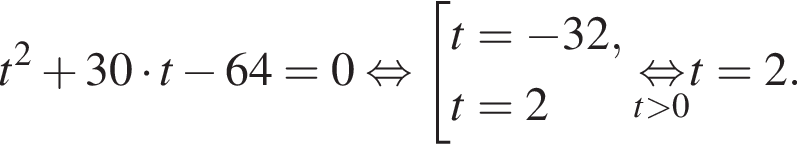
 Отсюда следует, что сумма корней уравнения равна 65.
Отсюда следует, что сумма корней уравнения равна 65.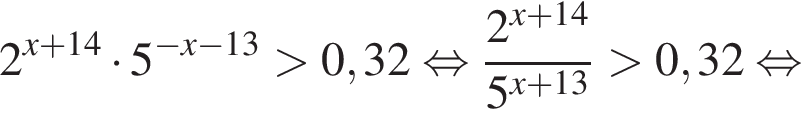
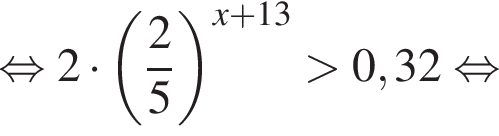
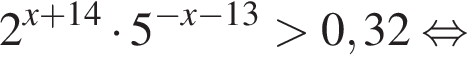
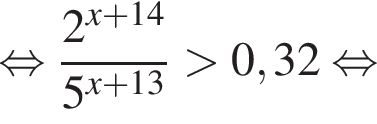
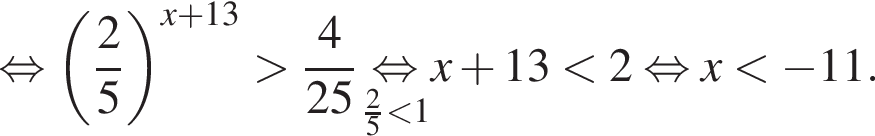
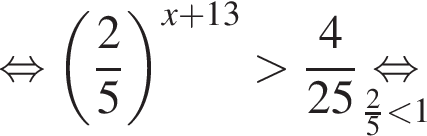
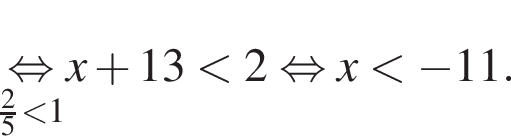
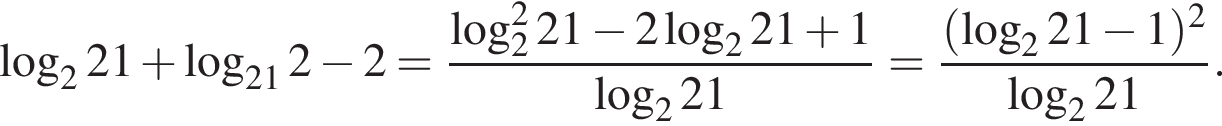
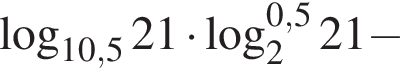
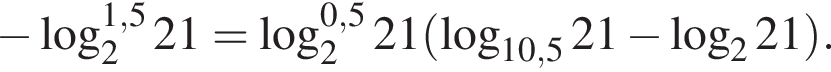
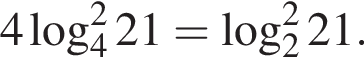 Тогда имеем:
Тогда имеем: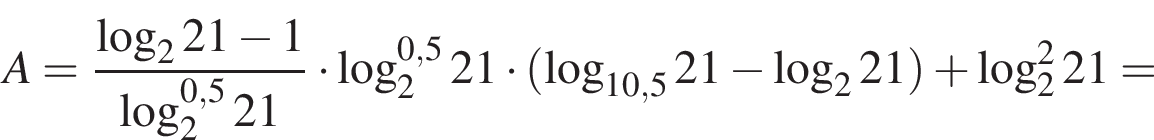
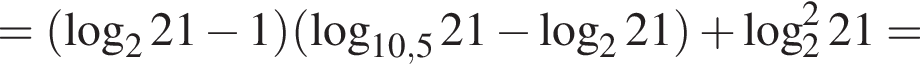
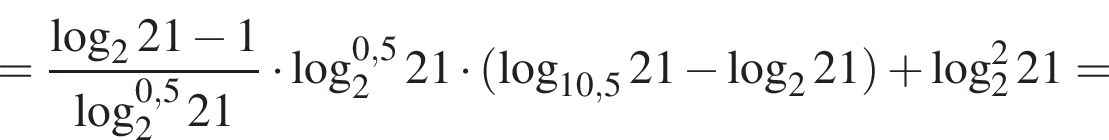
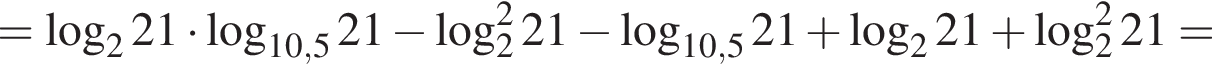
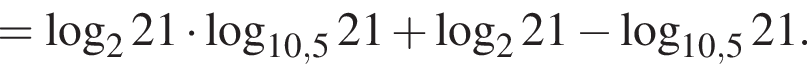
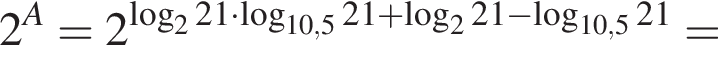
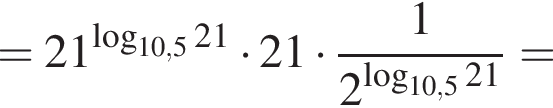
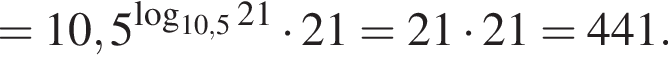
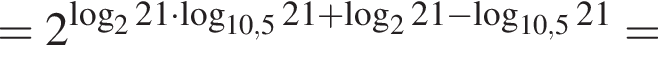
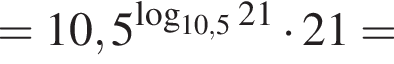
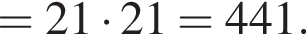
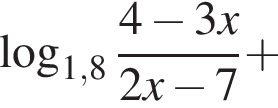
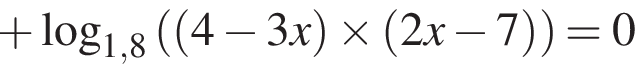
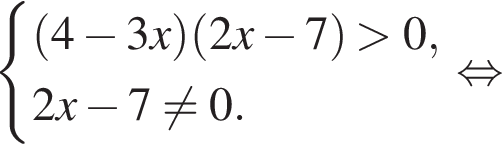
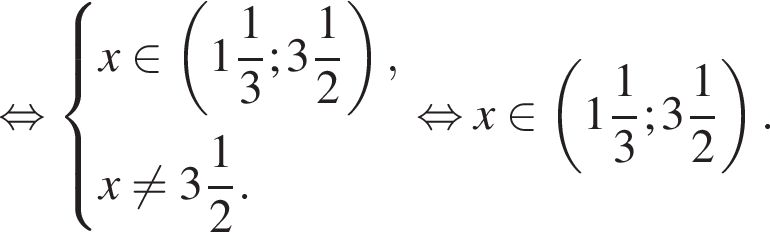
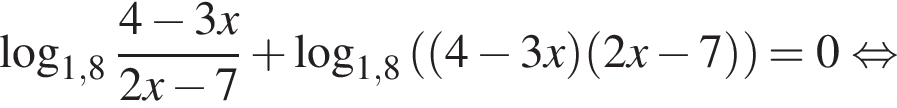
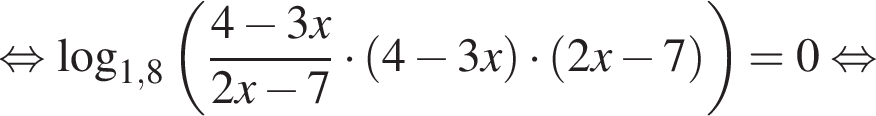
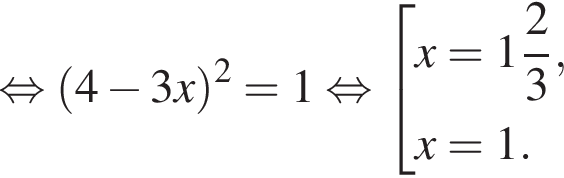
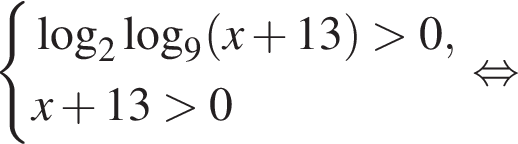
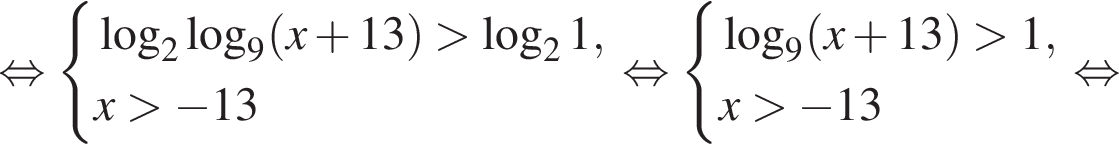
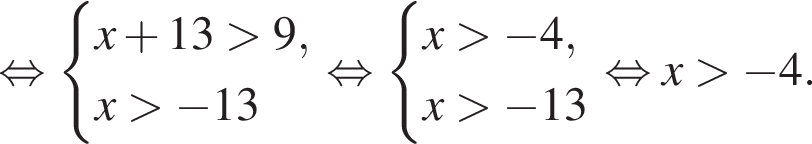
 тогда:
тогда: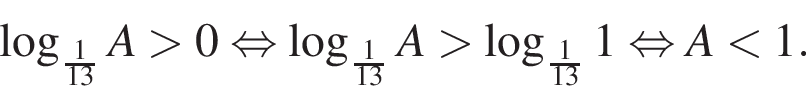
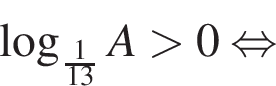
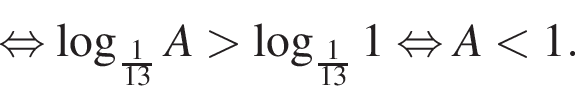

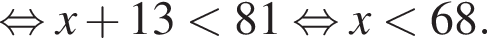

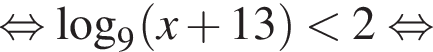
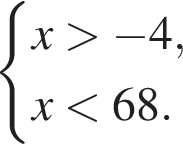 Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.
Поэтому наибольшее целое значение — 67, наименьшее целое значение −3, их сумма равна 64.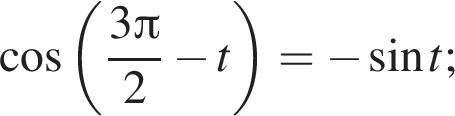
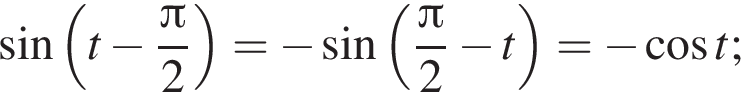
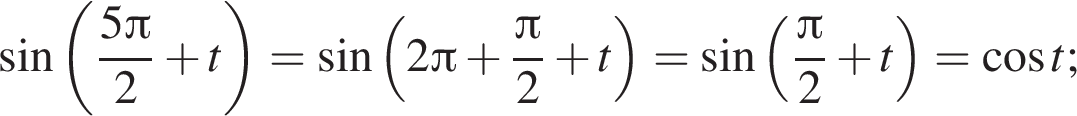
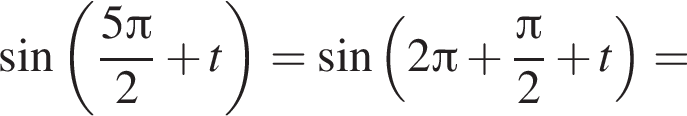
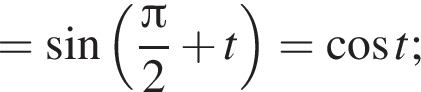
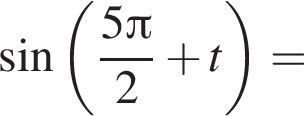
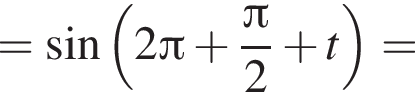
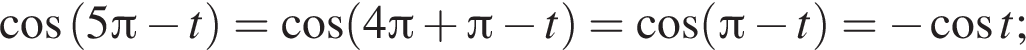

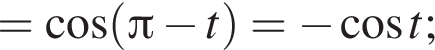
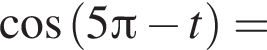
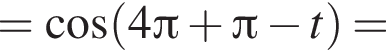
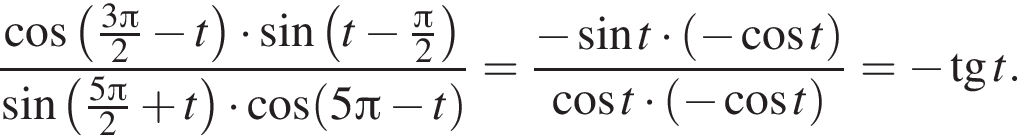
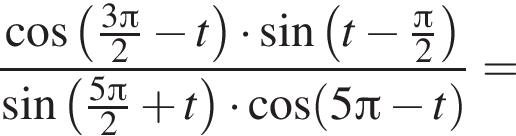
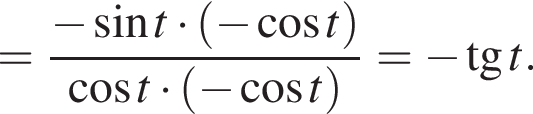
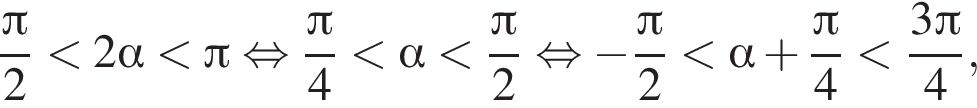

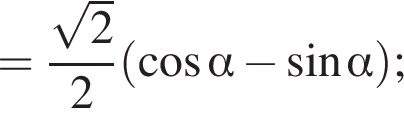
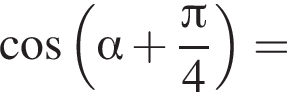
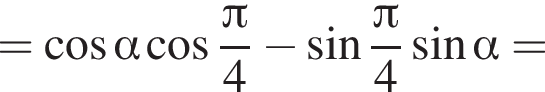
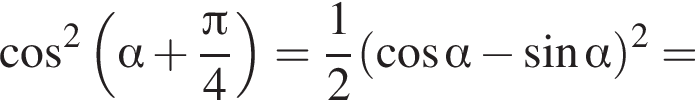

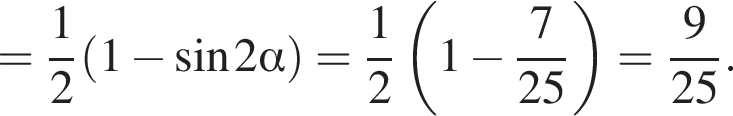
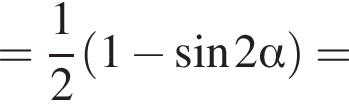
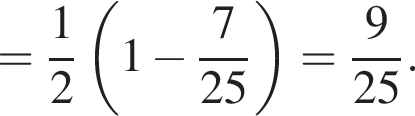
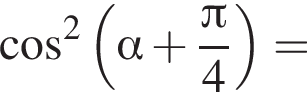
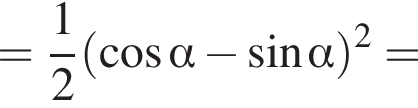
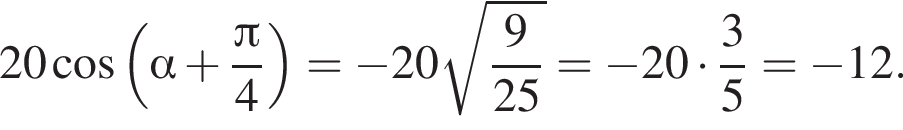
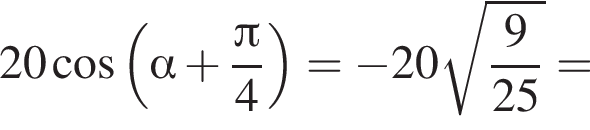
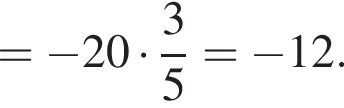
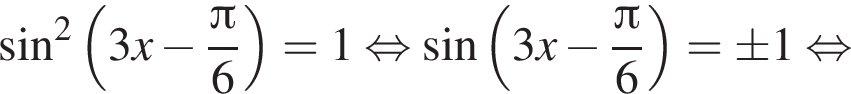
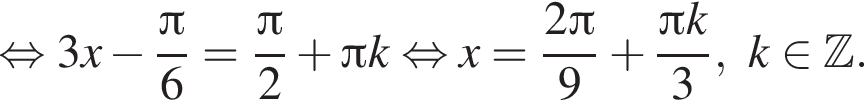
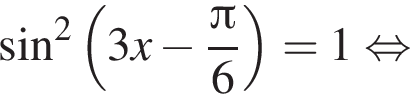
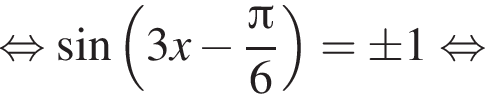
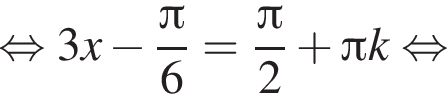
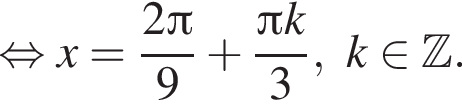
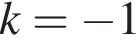 и равен
и равен 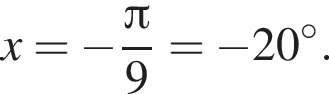
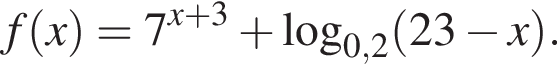 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 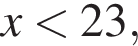 и что на
и что на 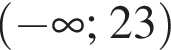
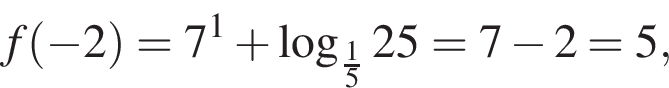 неравенство верно для всех x из
неравенство верно для всех x из 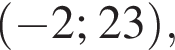 который содержит 24 целых числа.
который содержит 24 целых числа.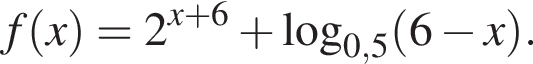 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 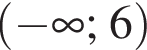
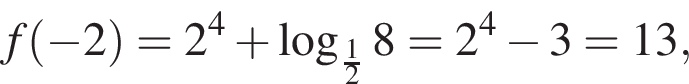 неравенство верно для всех x из
неравенство верно для всех x из 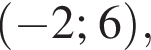 который содержит 7 целых чисел:
который содержит 7 целых чисел: 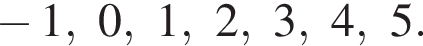
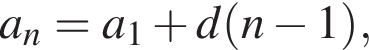 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 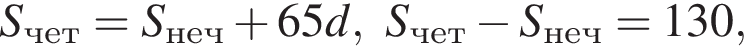 откуда
откуда 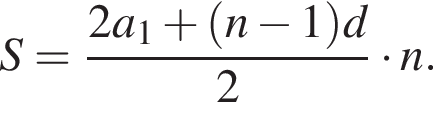 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: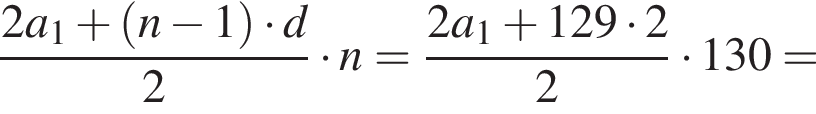
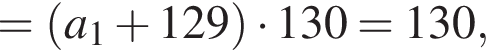
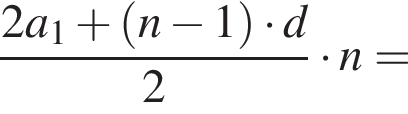
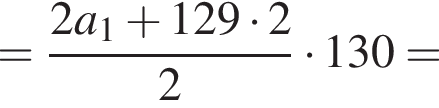
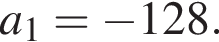 Получим
Получим 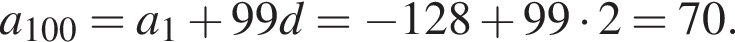
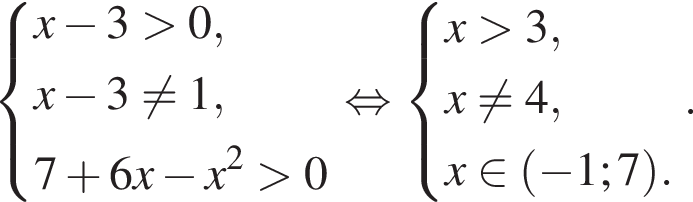
 представляет собой прямую, проходящую через точки вида
представляет собой прямую, проходящую через точки вида 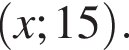 Таким образом, единственное подходящее решение — точка N.
Таким образом, единственное подходящее решение — точка N.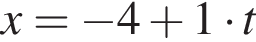 (м) и
(м) и 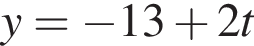 (м).
(м).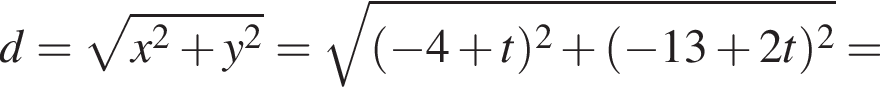
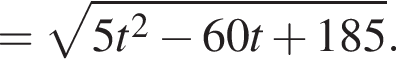
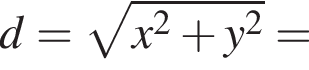
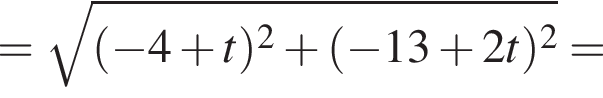
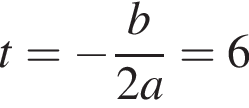 и в этой точке положительно:
и в этой точке положительно: 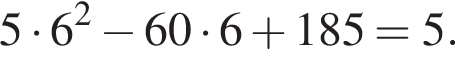 Таким образом, при
Таким образом, при 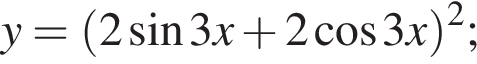


 имеем:
имеем:

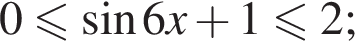
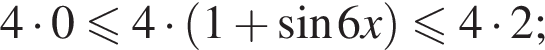
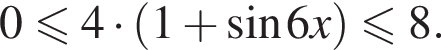
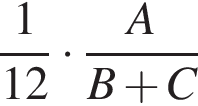 работы.
работы. 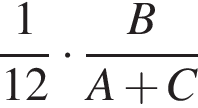 работы.
работы. 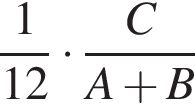 работы.
работы. 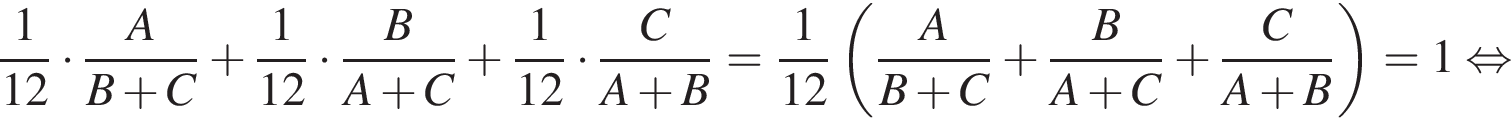
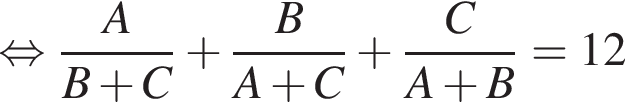
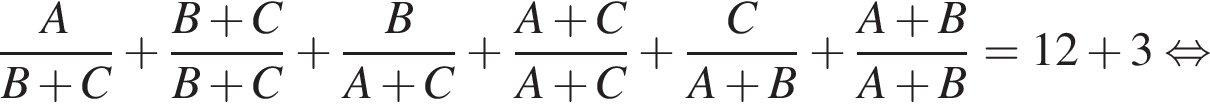
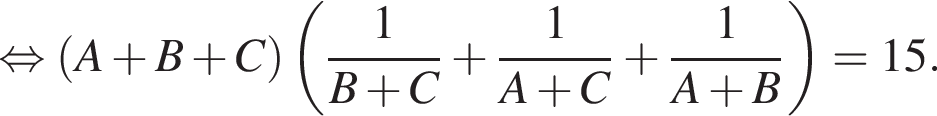
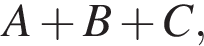 то они выполнили бы работу за:
то они выполнили бы работу за: 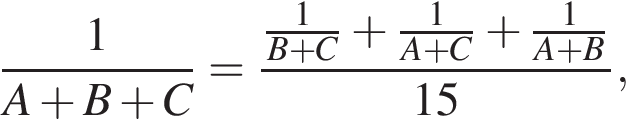
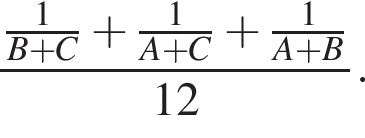 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 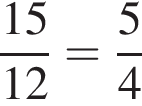 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число 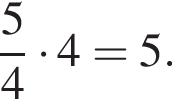
 Тогда:
Тогда: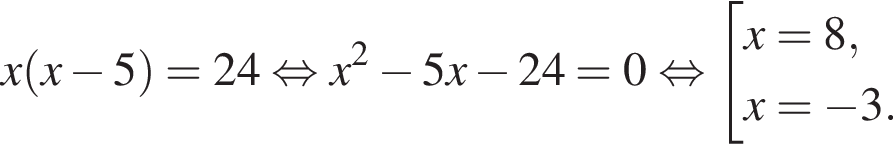
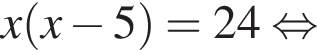
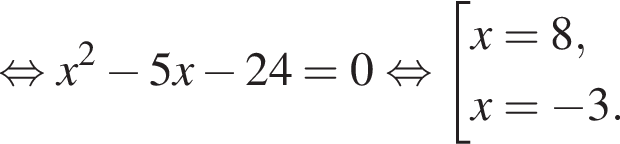

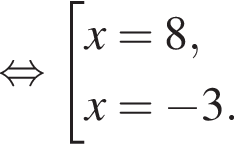
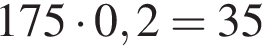 л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит:
л краски. Можно купить 3 банки по 10 литров и 2 банки по 2,5 литра, тогда минимальная сумма составит: